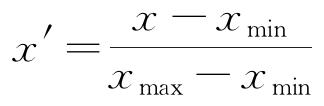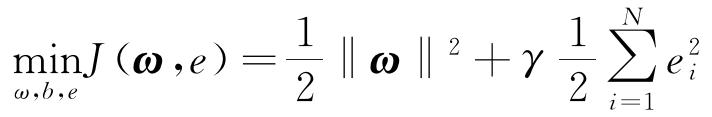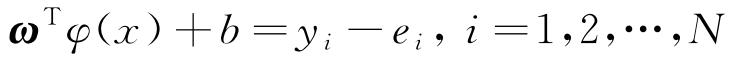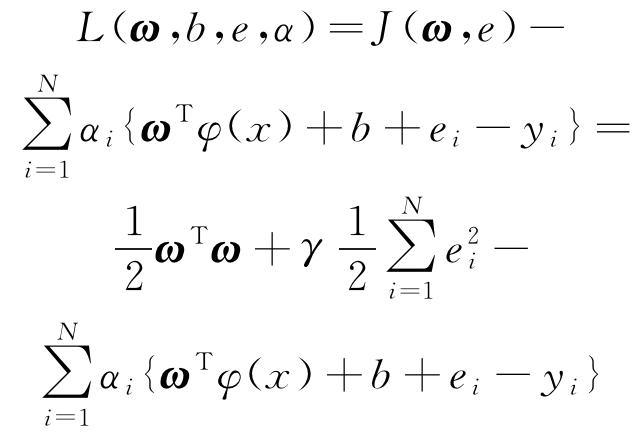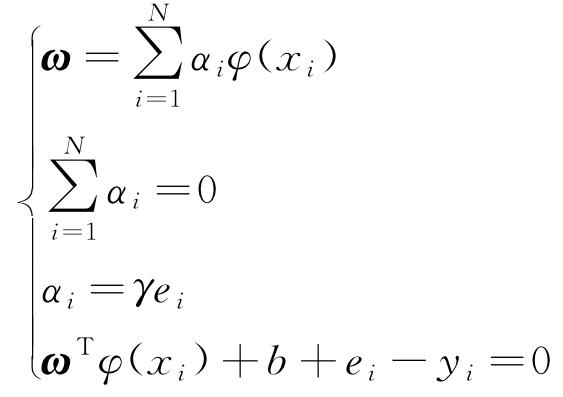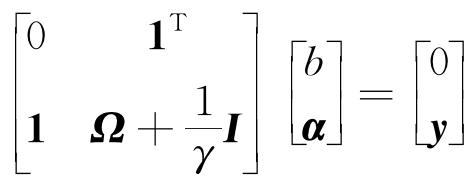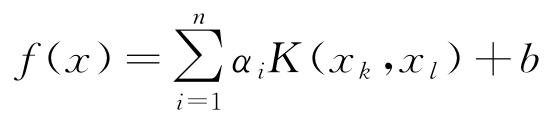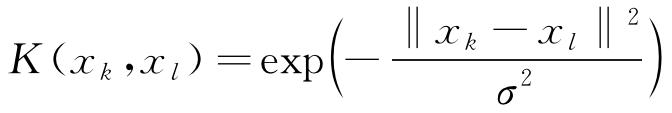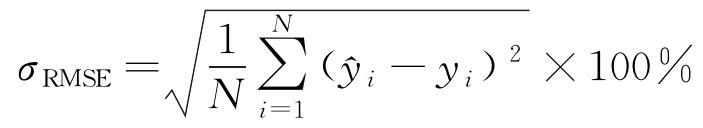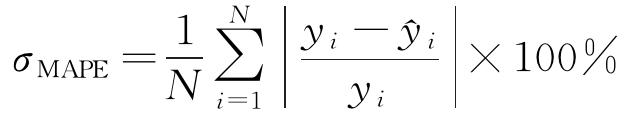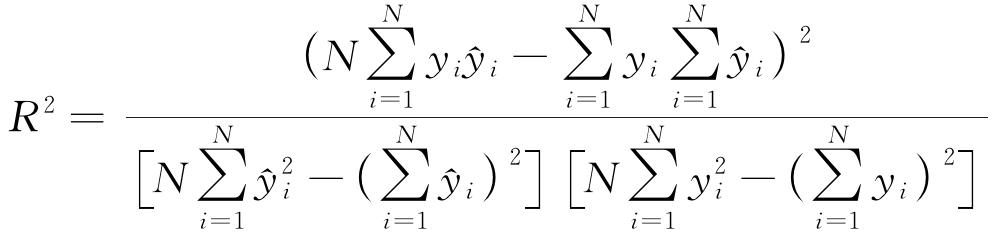基于粒子群优化和最小二乘支持向量机的储罐腐蚀速率预测

2024-12-13 14:25:27 作者：王明慧, 党鹏飞, 杨铮鑫, 龚博来源：腐蚀与防护分享至：

储罐是油气储运的主要设备,也是储存战略能源物资的重要装置,广泛应用在港口、化工、石油等行业。在储罐运行过程中,受储罐内介质和自然环境的影响,储罐局部构件不可避免发生腐蚀。随着储罐使用时间的延长,储罐的腐蚀会逐渐加剧,这将威胁储罐的安全使用。若能预测储罐的腐蚀速率,就可以提前采取防腐蚀措施,保障储罐的安全运行,避免经济损失。

目前,国内研究人员针对储罐内腐蚀行为进行了大量的研究,且取得了比较丰硕的研究成果。蒋林林等[1]对储罐底板进行声发射检测评价,并与开罐实测结果进行对比,发现声发射检测的结果与开罐实测的结果基本一致。穆大鹏等[2]将磁记忆检测技术应用在储罐罐壁腐蚀缺陷检测中,该技术能反映腐蚀缺陷位置等基本特征。刘文才等[3]基于Lamb波的反射/透射信号幅值比系数法对储罐罐顶腐蚀深度进行了检测,成功地将某石化基地的储罐罐顶腐蚀程度划分为轻微、中等和严重三个腐蚀等级。朱吉新[4]发现储罐沉降水中含有大量的Cl-、S2-和细菌等,造成储罐底板点蚀,防腐蚀涂层与牺牲阳极联合保护对储罐底板具有良好的保护效果。刘琪华等[5]基于遗传算法优化BP神经网络(GA-BP)和BP神经网络两种方法对储罐底板腐蚀情况进行了评估,结果表明GA-BP神经网络具用更高的腐蚀评估精度。张颖等[6]基于统计分析和专家经验得到了储罐底板腐蚀的主要外部因素,并运用贝叶斯网络对储罐底板的腐蚀状态进行了预测,通过与声发射检测结果对比可知预测结果的准确率达到87.5%。刘雪云等[7]运用广义极值分布作为储罐底板腐蚀深度最大值的统计模型,利用L矩阵计算相应参数,发现Weibull分布比Gumbel分布能更好地拟合储罐底板最大腐蚀深度的统计规律。朱本廷等[8]在灰色模型基础上提出非等间距的灰色模型,并对储罐的罐底、罐顶和罐壁的腐蚀速率分别进行了预测,发现改进的灰色模型对三个位置腐蚀速率的预测精度都达到了1级。

国内对储罐腐蚀的研究主要关注于储罐腐蚀状态的检测和最大腐蚀深度的分布规律。为此,作者利用粒子群优化(PSO)算法的全局寻优能力,对最小二乘支持向量机(LSSVM)的正则化参数和核参数进行优化,提出了一种基于粒子群优化和最小二乘支持向量机的储罐腐蚀速率预测方法,并采用储罐内腐蚀速率的实测数据对该方法的有效性进行了验证。

1. PSO-LSSVM模型

1.1 模型构建

基于粒子群优化和最小二乘支持向量机对储罐腐蚀速率预测的具体步骤可分以下几步。

1.1.1 获取并处理样本

获取运行中储罐历年的腐蚀速率样本D={(xi,yi)|(i=1,2,…,N}。其中,xi∈Rn,为n维输入样本；yi∈R,为xi对应的目标输出。为便于后续运算、减小奇异数据对预测结果的影响,使各样本数据处在同一数量级,需要先将原始数据按式(1)进行归一化处理,然后将归一化处理后的储罐腐蚀速率样本分为训练集和测试集两部分。

(1)

式中：x为原始数据；x'为归一化处理后数据；xmax和xmin依次为原始数据集中的最大值和最小值。

1.1.2 构建LSSVM

支持向量机是一类面对小样本的非线型机器学习算法。该算法采用一种非线性映射,把样本的低维特征反映到某个高维特征空间,进而获得高维空间中的线性回归,即将简单不确定性问题转换为线性问题的高维空间。LSSVM是在支持向量机的基础上采用等式约束取代不等式约束,因此减少了二次回归问题,使计算的准确度更高,运算效率更快。

LSSVM在高维空间中的线性回归函数可以表示为[9-11]

(2)

式中：ω为权向量；b为偏差量；φ(x)核空间映射函数。

基于结构风险最小准则,将LSSVM的回归问题转化为式(3)所示凸优化问题。

(3)

约束条件：

式中：ei为随机误差；γ正则化参数。γ值过高,易使拟合结果出现过拟合,γ值过小,则易使拟合结果出现欠拟合,因此合理的γ取值可使所求的函数具有较好的推广能力。

由于优化问题计算过程繁琐且计算量大,通常将式(3)转化为对偶问题,并引入Lagrange乘子对式(4)进行求解。

(4)

式中：αi为Lagrange乘子。根据KKT(Karush-Kuhn-Tucker)最优化条件[12],分别对式(4)中的变量ω,b,e,α求偏导数,得

(5)

消去ω和ei,可得到线性方程组

(6)

式中：I为单位矩阵；；；；；；。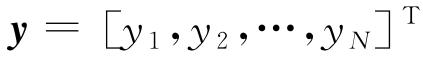

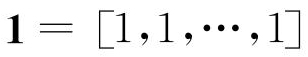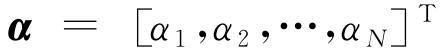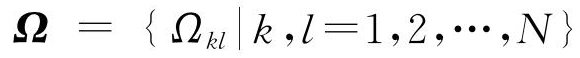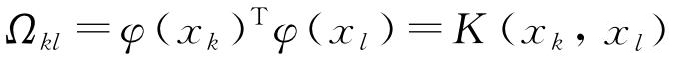根据式(2)~(6)整理可得LSSVM函数为

(7)

式中：αi为支持向量；K(xk,xl)为核函数,此处选用径向核函数(RBF),其表达式为

(8)

式中：σ2为核参数。

1.1.3 初始化PSO

设置LSSVM中的正则化参数γ和核参数σ2的取值范围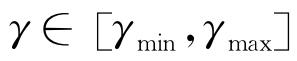和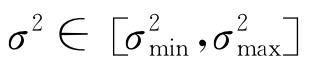,将一组参数序列(γ,σ2)作为PSO中粒子的初始位置向量,由训练集对LSSVM进行训练学习,构建测试样本的均方根误差作为PSO的适应度函数。

1.1.4 更新粒子的位置和速度

计算更新后粒子的适应度值,选出这一代的最优粒子并与上一代的最优粒子的适应度值进行比较,判断粒子是否需要再更新。PSO是一种全局优化算法,灵感来自鸟群在觅食流程中的迁徙和聚集行动[13-18]。在PSO算法中,所有解都被看作一组同时具有初始速率和初始位置的微粒。在所有粒子给出了起始位移和起始速率后,就可以开始进行迭代寻优,每个粒子通过追踪个体最优和全局最优来更新自己在解空间中的位置和速率。

1.1.5 判断是否达到最大迭代次数

若迭代次数达到最大,则输出最优参数组合(γ,σ2)并以此构建PSO优化的LSSVM预测模型；若迭代次数未达到最大,返回式(4)。具体流程如图1所示。

图 1 PSO-LSSVM流程图

Figure 1. Flow chart of PSO-LSSVM

1.2 模型精度检验

为了检验PSO-LSSVM模型的精度,选取均方根误差(σRMSE)、平均绝对百分误差(σMAPE)、决定系数(R2)三种指标检验模型的精度[19],计算公式如式(9)~(11)所示。

(9)

(10)

(11)

式中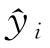：为第i年储罐底板内腐蚀速率的预测值；yi为第i年储罐底板内腐蚀速率的测量值；N为样本数据的个数。

计算每个粒子的适应度值,选择适应度值最小的粒子作为最优粒子。R2∈[0,1],R2越接近1,表明模型的拟合优度越高,模型的性能越好。σRMSE和σMAPE指标均在[0,1]范围内,数值越接近0,说明误差越小,预测效果越好。

2. 实例分析

2.1 数据选择

表1列出了某公司2008年到2020年某一储罐罐底、罐顶、第一层罐壁内腐蚀速率数据[20]。分别选择这组数据中的前70%作为训练样本数据,最后30%作为测试样本数据。

表 1 储罐罐底、罐顶和第一层罐壁的内腐蚀速率

Table 1. Corrosion rates of bottom, top and the first wall of tank

年份	内腐蚀速率/(mm·a-1)
年份	罐顶	第一层罐壁	罐底
2008	0.03	0.01	0.05
2009	0.07	0.04	0.12
2010	0.13	0.09	0.19
2011	0.19	0.11	0.26
2012	0.24	0.16	0.31
2013	0.27	0.21	0.38
2014	0.31	0.27	0.45
2015	0.36	0.31	0.52
2016	0.42	0.35	0.58
2017	0.49	0.38	0.64
2018	0.53	0.42	0.69
2019	0.57	0.49	0.73
2020	0.64	0.58	0.82

PSO粒子群数为30,最大迭代次数为300,正则化参数γ的取值为[10-2, 103],核参数的取值为[10-2, 102]。模型在训练中的迭代过程如图2所示。结果表明,该方法在优化过程中可以多次跳出局部最优,快速获得全局最优解。

图 2 罐底PSO-LSSVM迭代进化过程

Figure 2. Iterative evolution process of PSO-LSSVM for tank bottom

2.2 预测结果分析

将通过PSO得到的最优参数γ和σ2代入到LSSVM中对储罐罐底腐蚀速率进行预测。为了验证PSO-LSSVM的预测效果,同时采用LSSVM和PSO-SVM模型对储罐罐底腐蚀速率进行预测,并对三种模型的预测结果进行了比较。表2为采用三种模型预测的储罐罐底腐蚀速率。图3为三种模型罐底腐蚀速率预测结果的相对误差。可以发现,在PSO-LSSVM、LSSVM和PSO-SVM三种模型中,PSO-LSSVM的预测值和真实值的差距较小,且PSO-LSSVM预测结果的相对误差的波动小于其他两种方法,这表明PSO-LSSVM的预测效果最佳。

表 2 储罐罐底腐蚀速率的预测结果和实测结果

Table 2. Predicted results and test results of corrosion rate of tank bottom

年份	实测腐蚀速率/ (mm·a-1)	预测腐蚀速率/(mm·a-1)
年份	实测腐蚀速率/ (mm·a-1)	PSO-LSSVM	LSSVM	PSO-SVM
2017	0.64	0.631 69	0.635 79	0.641 74
2018	0.69	0.690 89	0.692 31	0.706 25
2019	0.73	0.748 22	0.745 23	0.770 59
2020	0.82	0.813 41	0.794 13	0.834 72

图 3 三种模型罐底腐蚀速率预测结果的相对误差

Figure 3. Relative error comparison of tank bottom prediction results

运用同样的方法分别对储罐的罐顶和第一层罐壁进行腐蚀速率预测,预测结果见表3。为了更进一步了解PSO-LSSVM的预测精度,运用上文中提到的均方根误差、平均绝对百分误差、决定系数三种统计学指标对三种预测模型进行评价,评价结果见表4。

表 3 储罐罐顶和罐壁第一层腐蚀速率的预测结果和实测结果

Table 3. Corrosion rate prediction results of tank roof and the first layer of tank wall

年份	罐顶的腐蚀速率/(mm·a-1)				第一层罐壁的腐蚀速率/(mm·a-1)
年份	实测值	PSO-LSSVM预测值	LSSVM预测值	PSO-SVM预测值	实测值	PSO-LSSVM预测值	LSSVM预测值	PSO-SVM预测值
2017	0.49	0.473	0.450	0.453	0.38	0.388	0.394	0.389
2018	0.53	0.533	0.489	0.495	0.42	0.443	0.437	0.432
2019	0.57	0.585	0.524	0.537	0.49	0.499	0.479	0.474
2020	0.64	0.624	0.556	0.577	0.58	0.563	0.519	0.515

表 4 三种模型预测性能指标对比

Table 4. Comparison of predicted performance indexes of the three models

模型	罐顶			第一层罐壁			罐底
模型	σMAPE/%	σRMSE/%	R2	σMAPE/%	σRMSE/%	R2	σMAPE/%	σRMSE/%	R2
PSO-LSSVM	2.265	0.010	0.973	3.077	0.012	0.982	1.18	0.011	0.976
LSSVM	9.264	0.155	0.965	5.134	0.055	0.966	1.71	0.016	0.955
PSO-SVM	7.469	0.097	0.944	4.903	0.059	0.970	2.50	0.023	0.967

从平均绝对百分误差来看,罐顶、第一层罐壁和罐底PSO-LSSVM的结果比LSSVM和PSO-SVM的结果分别减少了6.99%、2.057%、0.53%和5.198%、1.826%、1.32%；从均方根误差来看,罐顶、第一层罐壁和罐底PSO-LSSVM的结果比LSSVM和PSO-SVM的结果分别降低了0.145%、0.043%、0.005%和0.087%、0.047%、0.012%；罐顶、第一层罐壁和罐底PSO-LSSVM预测结果的决定系数分别为0.973、0.982、0.976,均高于另外两种方法。以上分析结果均进一步说明PSO-LSSVM的预测精度是三种模型中最高的。