长期暴露于大气腐蚀环境中的钢结构极易遭受锈蚀损伤,造成构件承载面积损失和材料性能劣化,严重影响结构的后续服役性能与安全性,Kinzua铁路桥[1]和Silver桥[2]的倒塌进一步凸显了腐蚀问题在结构工程中的严峻性。锈损钢结构安全性评估很大程度上依赖腐蚀本身的量化,腐蚀速率与表面统计特征是准确把握腐蚀特征的重要前提,也是可靠性分析的基础数据,腐蚀速率宏观把握腐蚀量的发展趋势,反映了构件承载面积损失,而表面统计特征则体现腐蚀特征的空间变异性,揭示了结构钢力学性能退化的原因。
早在20世纪初,国内外学者便围绕钢材腐蚀速率开展了一系列研究工作。Albrecht和Hall[3]对大气环境下结构钢腐蚀性进行研究并总结了腐蚀损失规律。叶堤等[4,5]和杨熙珍等[6]探讨了我国大气环境对结构钢腐蚀速率的影响。考虑到腐蚀速率并非一成不变[7],学者们还提出了多种腐蚀速率模型,如双线性[8]、三段式[9]和幂函数模型[10]等。在既有结构领域,近些年人们逐渐认识到腐蚀表面特征是造成结构钢力学性能退化的主要原因[11],如何表征和模拟腐蚀表面的不规则性与随机性成为广泛关注的问题。而实现上述目的,则必须依赖精细的采集分析方法和数学表征模型。
随着扫描电子显微(SEM)测试[12]、原子力显微(AFM)测试 [13,14]、X射线断层成像[15]、激光共聚焦显微(CLSM)测试 [16,17]、白光干涉三维扫描(WLI) [18,19,20]等光学测量技术的发展,形貌分析开始应用于腐蚀表征,并使得锈坑精确分析成为可能。为提高分析效率,研究人员通常自行编制形貌分析程序,但通用性往往不强,尤其在锈坑识别与参数提取方面存在许多弊端。Wang和Cheng[16]采用图形识别(imfindcircles)算法对CLSM采集表面进行锈坑宽度提取,但仅能识别理想圆形锈坑且无法确定锈坑深度等三维信息;Holme和Lunder[18]借助自编程序引导WLI仪器识别锈坑位置并确定其深度、宽度等,但仅适合于点蚀早期特征的精细化分析。
在锈蚀钢材表面统计特征方面虽已开展了许多研究工作,但缺少统一的腐蚀表面表征参数,且研究大多集中于海洋环境,包括锈蚀钢材表面腐蚀形貌[21]、分形特征[22]、粗糙度[20]、锈坑深度变化规律[23,24]、锈坑深度与径深比时变模型[25,26]等,而针对一般大气环境的研究却鲜有报道,尤其缺乏以建立腐蚀表面表征模型为目的、针对模型相关表征参数开展的统计分析工作。
腐蚀表面随机模型是对腐蚀统计特征的模型化,也是实现腐蚀表面模拟和重建的前提。Silva等[27]基于海洋环境腐蚀特征与Monte Carlo法重建了上千个腐蚀表面,但腐蚀变量均在各自区间内随机生成,忽略了变量统计特征与相关性。功率谱与随机场理论的引入[28,29,30]无疑为腐蚀深度随机模型的建立奠定了基础,邱斌[31]基于盐雾锈蚀钢材截面轮廓数据,提出了伪二维腐蚀深度随机场模型,但无法考虑腐蚀深度在各方向的相关性与相关长度,因而其重建形貌与真实形貌存在较大差别。Wang等[32]根据海洋环境下船体结构测量数据提出了锈坑分布模型,但忽略了锈坑形状变异性与参数统计规律,因而准确性难以保证。
综上所述,钢材腐蚀速率研究已趋于成熟,但一般大气环境下钢材腐蚀表面统计特征与随机模型研究仍十分欠缺,现有随机模型由于本身存在内在缺陷,往往难以准确反映其表面特征。针对上述问题,本工作通过一般大气环境加速/自然腐蚀实验与表面特征采集分析,旨在揭示一般大气环境结构钢锈蚀深度与锈坑特征统计规律,由此提出结构钢腐蚀表面精细化表征方法与随机模型,从而实现腐蚀表面的准确模拟与重建,为锈损钢结构可靠性评估提供数据支持。
1 实验方法
1.1 腐蚀实验与表面形貌测定
参照《金属和合金的腐蚀——户外周期喷淋暴露试验方法》(GB/T 24517-2009),采用室外周期自动喷淋装置对无涂层Q235B钢板进行0、40、80、120、160、240、320 d加速腐蚀实验,试件编号分别为A0~A6。考虑到一般大气环境中的腐蚀介质主要为硫化物与氯化物,并与近海环境相区别,实验采用质量分数为0.2%的Na2SO4弱酸性溶液,pH值为5.5。装置每15 min喷淋一次,24 h为一周期,每7 d翻转试件一次,保证两面腐蚀程度一致。试件按龄期取出并采用机械方法除锈,腐蚀程度由失重率(γ)进行初步衡量。
为研究自然环境下钢材的腐蚀状态,从某自然暴露8 a的钢架(Q235B)中截取了部分试件。试件分别来源于水平杆(H)、竖杆(V)和斜杆(S)的上翼缘(TF)、下翼缘(BF)和腹板(W),并按照构件及板件位置对截取试件进行分组编号。
借助PS50三维非接触表面形貌仪,对6块加速腐蚀钢板和9块自然腐蚀钢板进行表面形貌测定,测量区域分别为25 mm×15 mm、50 mm×25 mm,纵横向扫描步长为50 μm,扫描数据为501×301、1001×501的规则网格。由于试件上下表面(A、B)分别扫描,需采用测厚规测量上下表面最大残余厚度(Tmax),从而确定相对位置。由于锈蚀钢材原始表面未能保留,仪器默认最高点为参考面,即锈蚀深度为相对值。
1.2 腐蚀表面表征参数与提取方法
一般大气环境下,钢材将出现全面腐蚀和局部腐蚀特征,外部腐蚀条件与材料自身差异还会导致2种行为交叉出现,合理表征腐蚀特征必须对锈蚀深度和锈坑特征分别进行讨论。近年来,针对锈蚀深度和锈坑特征的表征参数相继提出。如孔正义[33]利用W-M分形模型对腐蚀钢材表面进行模拟,商钰[34]统计了锈蚀钢材局部最大腐蚀深度和粗糙度等。Xu等[35]提出了结构钢锈坑尺寸参数、形状参数和统计参数。
用于表征钢材腐蚀表面特征的参数众多,但许多参数关联性差,有些则物理含义重复。以较少的参数准确实现腐蚀表面表征与还原、且易于建立腐蚀表面模型是选取表征参数的基本原则,由此本工作提出用于锈蚀钢材表面表征的基本参数:(a) 锈蚀深度参数,包括平均锈蚀深度(Δtave)、锈蚀深度标准差(tsd);(b) 锈坑参数,包括锈坑深度(h)、锈坑径深比(Ar)、锈坑体积比(VB)、锈坑密度(Pd)。
鉴于表面形貌可以直观全面反映腐蚀水平,本工作提出基于腐蚀形貌的表征参数提取方法,并借助MATLAB平台开发了相应的计算程序CroEva。
腐蚀表面扫描结果为规则的矩形网格,Δtave和tsd由下式计算:
Δtave=∣∣∣z̅∣∣∣=1MN∑i=1M∑j=1N∣∣z(xi, yj)∣∣
(1)
tsd=1MN⎛⎝∑i=1M∑j=1N(z(xi, yj)-z̅)2⎞⎠−−−−−−−−−−−−−−−−−−−−−−−⎷
(2)
式中,M、N分别为x、y方向上扫描点的数量;z(xi, yj)为扫描点纵坐标值,z̅为扫描点纵坐标平均值。需指出,扫描结果默认腐蚀表面最高点z坐标值为0,因此最高点与均值平面的距离为Δtave,即Δtave同样表示非均匀锈蚀深度平均值,如图1所示。由式(1)和(2)可知,Δtave、tsd与ISO25178-2-2012定义的粗糙度参数Sa、Sq物理意义相同,分别表示粗糙表面的算术平均偏差与均方根偏差。
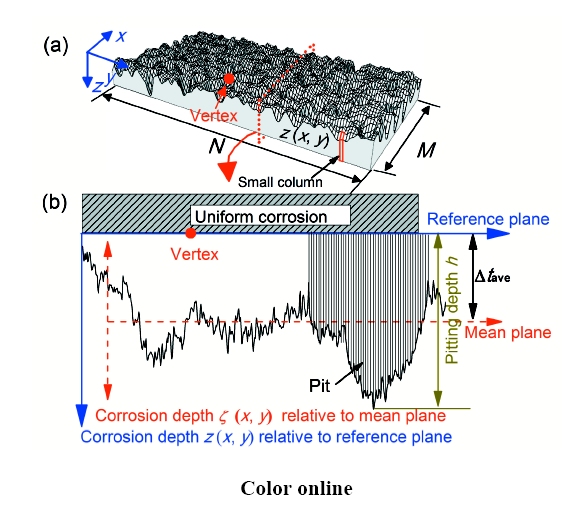
图1 锈蚀深度参数提取示意图
锈坑参数提取程序原理如图2a所示,CroEva程序沿高度自上而下创建二值化切片图像,通过泛洪填充(Floodfill)算法确定孤立区域(锈坑)并进行标记和编号,随后计算相应的锈坑参数,提取结果见图2b。由于锈坑形状不规则,约定采用某一孤立区域内z方向上最大深度作为h,x、y方向上孤立区域尺寸的平均值作为锈坑直径(R)。锈坑形状由VB反映:
VB=Vp/Vrec
(3)
⎧⎩⎨⎪⎪Vp=∑i=1Np|zave(i)|S2Vrec=RxRyh
(4)
式中,Vp为锈坑体积;Vrec为包围锈坑的最小长方体的体积;Np为锈坑内小柱体(图1a)的数量,即(M-1)(N-1);zave(i)为小柱体4个角点纵坐标的平均值;S为扫描步长;Rx、Ry分别为x、y方向上的锈坑直径。锈坑形状与VB值存在如下对应关系[36]:VB(cone)=π/12;VB(hemisphere)=π/6;VB(cylinder)=π/4;VB(cuboid)=1。

图2 锈坑参数提取原理示意图与提取结果
2 实验结果及分析
2.1 腐蚀程度与表面形貌
表1给出了所有试件的腐蚀程度。可以看出,加速腐蚀试件锈蚀率(γ)为2.76%~12.56%,自然腐蚀试件γ为16.94%~32.99%。加速腐蚀试件的γ随腐蚀龄期逐渐增大,当γ>4%时,最大残余厚度(Tmax)<初始厚度(T0),均匀腐蚀开始出现。对于自然腐蚀试件,水平杆(H)及斜杆(S)锈蚀率明显大于竖件(V),说明构件位置对锈蚀程度具有较大影响;由于腹板本身厚度较薄,其锈蚀率相对较大。
表1 试件腐蚀程度参数
Table 1 Corrosion degree parameters of steel plates
Corrosion condition Sample No. Corrosion time T0 / mm Tmax / mm γ / % Δte / μm
Accelerated corrosion A1 40 d 7.2 7.20 2.76 199
A2 80 d 7.2 7.20 4.26 307
A3 120 d 7.2 7.14 6.04 435
A4 160 d 7.2 7.06 8.72 628
A5 240 d 7.2 7.03 9.07 653
A6 320 d 7.2 6.82 12.56 904
Natural corrosion HTF 8 a 9.0 7.98 21.18 1906
HBF 8 a 9.0 7.93 21.85 1966
HW 8 a 6.5 5.28 29.92 1944
STF 8 a 9.0 7.84 21.97 1977
SBF 8 a 9.0 7.80 22.64 2037
SW 8 a 6.5 5.27 32.99 2144
VTF 8 a 8.0 7.36 16.94 1355
VBF 8 a 8.0 7.25 19.21 1537
VW 8 a 6.0 5.42 19.73 1184
Note: H—horizontal component, S—sloping component, V—vertical component, TF—top flange, BF—bottom flange, W—web. T0—initial thickness, Tmax—maximum residual thickness, γ—mass loss rate, Δte=γT0—equivalent thickness loss. The initial weight of naturally corroded specimens was estimated based on the initial thickness and density
图3和4给出了加速腐蚀和自然腐蚀钢板试件的三维形貌扫描结果。对于加速腐蚀试件,腐蚀初期以肉眼可见的微小锈坑为主,随后微小锈坑逐渐融合,锈坑尺寸逐渐增大。对于自然腐蚀钢板,表面形貌更加不规则,大尺寸锈坑更容易出现在水平杆(H)及斜杆(S)上,尤其是翼缘下表面(Side B)及腹板,这是因为重力作用导致雨水积聚,延长了浸润时间[37,38];翼缘上表面(Side A)由于蒸发而常处于干燥状态,因而锈坑尺寸较小;竖杆(V)锈坑尺寸相对较小,但分布更加密集。
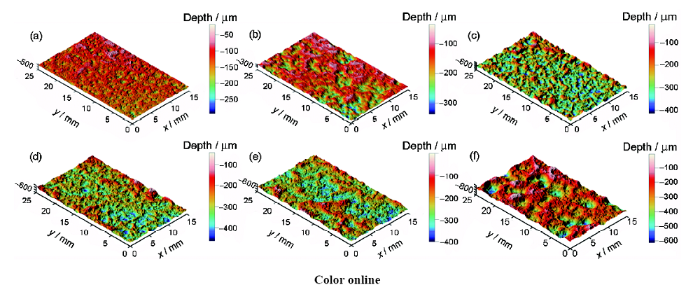
图3 加速腐蚀试件表面形貌
2.2 锈蚀深度分析
图5给出了部分加速腐蚀和自然腐蚀试件的锈蚀深度频率直方图,Δtave和tsd计算结果见表2。可以看出,锈蚀深度大致服从正态分布。对于加速腐蚀试件,龄期为40 d时(A1),锈蚀深度较小且主要分布于0~250 μm (图5a);龄期为320 d时(A6),锈蚀深度分布范围达到0~550 μm (图5c)。随着腐蚀时间的延长,锈蚀深度分布区间、Δtave、tsd均增大,说明锈蚀更加严重,表面更加粗糙。对于自然腐蚀试件,水平杆(H)和斜杆(S)更易遭受严重的全面腐蚀,锈蚀深度分布范围、Δtave和tsd均较大;而竖杆(V)则表现出更小的均值和标准差。
图4 自然腐蚀试件表面形貌
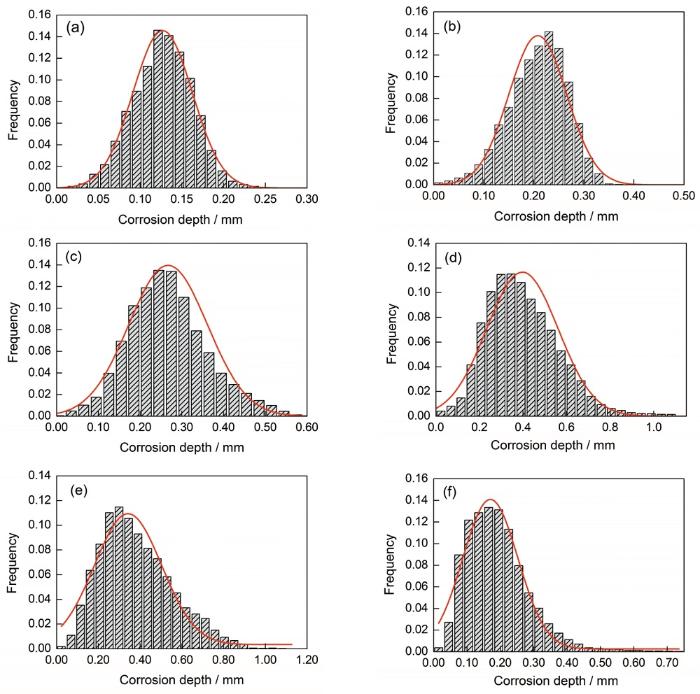
图5 加速腐蚀与自然腐蚀部分试件锈蚀深度频率分布直方图
表2 锈蚀深度参数统计结果
Table 2 Corrosion depth parameters of steel plates
Sample No.
Δtave / μm tsd / μm κ1 κ2
Side A Side B Side A Side B Side A Side B Side A Side B
A1 117 82 36 28 1.02 0.92 0.45 0.42
A2 173 134 58 46 0.98 1.05 0.50 0.46
A3 208 167 58 62 1.03 1.12 0.45 0.45
A4 243 245 64 78 1.24 1.28 0.60 0.58
A5 242 241 60 80 1.22 1.15 0.64 0.59
A6 267 257 94 87 1.39 1.48 0.75 0.70
HTF 310 576 138 186 2.47 2.48 0.95 1.06
HBF 397 500 164 177 2.34 2.28 0.97 1.10
HW 291 433 115 146 1.98 2.18 0.98 0.96
STF 284 533 156 180 2.79 2.50 0.89 1.02
SBF 340 498 157 167 2.08 2.15 1.13 1.15
SW 382 532 173 178 2.29 2.26 0.68 1.13
VTF 281 434 145 110 1.31 2.03 0.52 1.02
VBF 320 467 138 163 2.17 2.44 0.95 1.06
VW 397 207 164 90 2.24 1.52 0.97 0.56
Note: Δtave—mean value of corrosion depth, tsd—standard deviation of corrosion depth, κ1 and κ2—fitting parameters of power spectrum for corroded surface
图6为根据实验结果给出的Δtave和tsd的变化规律。可见,Δtave随等效锈蚀厚度Δte(即γT0)呈增大趋势,但斜率逐渐降低,说明腐蚀后期非均匀锈蚀的比重逐渐减小,均匀锈蚀比重逐渐增加;tsd与Δtave呈线性关系,斜率大致为0.33,自然腐蚀试件与拟合曲线的偏差较大,其原因可能与试件截取自不同位置有关。
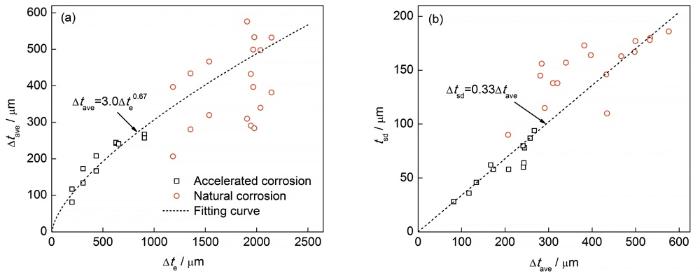
图6 平均锈蚀深度(Δtave)和锈蚀深度标准差(tsd)的变化规律
功率谱分析是研究表面特征的重要方法,其可以反映表面纹理方向性和不同波长对表面粗糙度均方根高度的影响[28]。在开展功率谱分析前,参考图1b将锈蚀深度数据z(x, y)处理成均值为0、方差为t2sd的样本函数ζ(x, y):
ζ(x, y)=z(x, y)+Δtave
(5)
并对形貌数据进行二维快速Fourier变换(FFT)。假定x、y方向上的扫描间隔分别为Δx、Δy,扫描点数量分别为M、N,则二维离散FFT可由下式求得[39]:
F(ω1p, ω2q)=∑m=0M-1∑n=0N-1ζ(mΔx, nΔy)⋅ exp[-2πi(pMm+qNn)]
(6)
式中,p=0, 1, …, M-1;q=0, 1, …, N-1;ω1p、ω2q分别为x、y方向上的第p、q个谐和分量波数(或圆频率),ω1p=2πp/(MΔx),ω2q=2πq/(NΔy),单位为rad/mm。离散二维双边谱密度S(ω1p, ω2q)由下式计算:
S(ω1p, ω2q)=ΔxΔy(2πM)(2πN)|F(ω1p, ω2q)|2
(7)
图7为部分加速腐蚀试件锈蚀深度二维双边功率谱密度计算结果。可以看出,腐蚀程度越大,功率谱密度峰值越高,谐和分量波数上限越小。由于腐蚀表面各方向呈现出相同的分布特征,可采用下式对锈蚀深度功率谱密度进行描述:
S(ω1, ω2)=t2sdκ214πexp[-(κ2ω1)2-(κ2ω2)2]
(8)
式中,κ1、κ2为与腐蚀程度相关的腐蚀表面功率谱拟合参数[40],κ1与功率谱密度峰值有关,κ2与谐和分量波数上限有关。表2汇总了κ1和κ2的拟合结果,图8给出了κ1、κ2变化规律。可以看出,参数κ1与Δtave呈幂函数关系;κ2在腐蚀初期基本不变(0.45),Δtave处于270~350 μm区间内时κ1迅速增加,而后趋于稳定(1.05)。
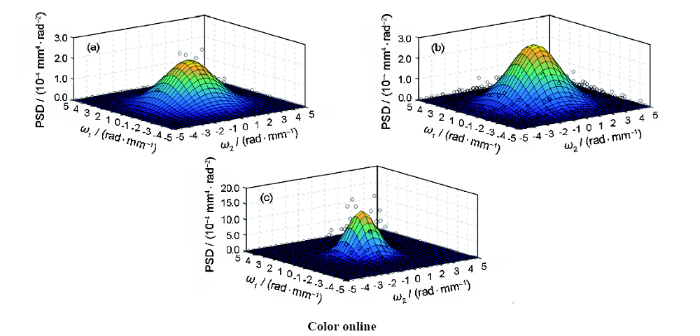
图7 部分加速腐蚀试件功率谱密度函数拟合结果
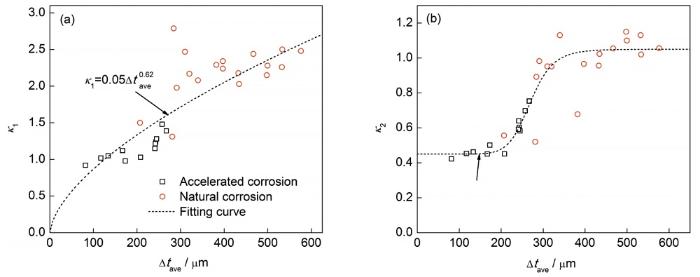
图8 与腐蚀程度相关的腐蚀表面功率谱拟合参数κ1和κ2变化规律
2.3 锈坑特征分析
图9给出了加速腐蚀和自然腐蚀试件时h和Ar提取结果。对于加速腐蚀试件,h区间随龄期逐渐增大,由40 d的72~213 μm增大至320 d的210~533 μm;Ar大致分布于0~12的区间上,分布范围逐渐减小。自然腐蚀试件h分布于100~1200 μm,除HTF和STF上表面(Side A)外,Ar大致分布于0~6。
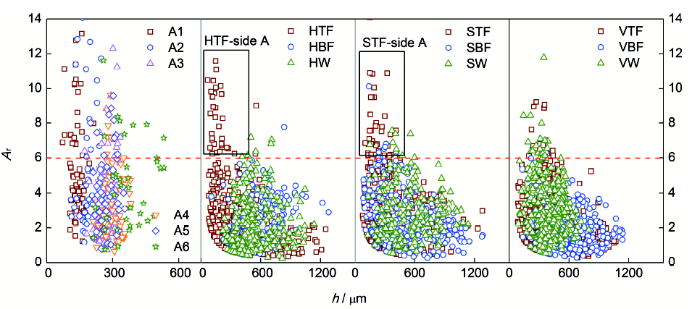
图9 锈坑深度(h)和径深比(Ar)提取结果
锈坑几何参数的分布形式主要有正态分布、对数正态分布、Weibull分布及指数分布[41]。通过对h和Ar进行假设检验发现,均较好地服从对数正态分布,参数估计结果见表3和图10。可以看出,随着腐蚀程度的增加,锈坑深度对数均值(μh)逐渐增大,对数标准差(σh)变化规律不明显,其值介于0.1~0.6;锈坑径深比对数均值(μAr)逐渐减小,对数标准差(σAr)基本不变,其值介于0.5~0.7。
表3 锈坑特征参数统计结果
Table 3 Characteristic parameters of corrosion pits of steel plates
Sample No.
Pd / cm-2 μh σh μAr σAr
Side A Side B Side A Side B Side A Side B Side A Side B Side A Side B
A1 22.2 19.1 4.91 5.09 0.19 0.16 1.58 1.55 0.55 0.53
A2 20.5 20.1 5.21 5.35 0.20 0.18 1.56 1.62 0.69 0.63
A3 19.4 18.5 5.68 5.51 0.07 0.10 0.90 1.43 0.61 0.59
A4 16.2 17.2 5.75 5.80 0.11 0.21 0.94 0.85 0.60 0.63
A5 12.5 13.2 5.63 5.82 0.13 0.14 1.21 0.92 0.64 0.66
A6 10.1 11.5 5.88 5.95 0.24 0.16 1.33 0.95 0.63 0.60
HTF 20.2 6.4 5.46 6.47 0.53 0.38 0.97 0.34 0.69 0.69
HBF 6.9 7.5 6.38 6.23 0.39 0.31 0.72 0.72 0.54 0.68
HW 9.4 11.5 6.34 5.98 0.34 0.21 0.16 0.25 0.5 0.53
STF 15.7 7.6 5.40 6.35 0.40 0.44 1.24 0.61 0.64 0.66
SBF 13.4 10.7 5.88 5.72 0.67 0.48 0.43 0.57 0.62 0.60
SW 8.6 6.8 5.89 6.46 0.38 0.36 1.07 0.68 0.51 0.51
VTF 15.3 14.6 5.49 5.80 0.47 0.63 0.58 0.24 0.49 0.62
VBF 11.0 13.3 6.09 6.27 0.50 0.34 0.28 0.24 0.56 0.56
VW 12.2 14.5 5.91 5.70 0.35 0.39 0.69 0.73 0.49 0.59
Note: Pd—pit density, μh and σh—logarithmic mean value and standard deviation of pit depth, μAr and σAr—logarithmic mean value and standard deviation of pit aspect ratio
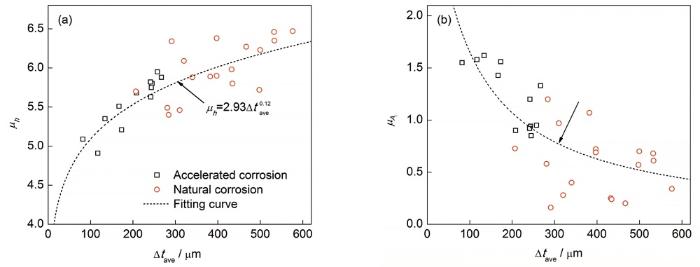
图10 锈坑深度对数均值(μh)和锈坑径深化对数均值(μAr)变化规律
图11给出了加速腐蚀和自然腐蚀试件体积比(VB)提取结果。对于加速腐蚀试件,频率峰值对应的VB随腐蚀龄期逐渐左移,由40 d的0.6降至240 d的0.3,即锈坑由圆柱体逐渐转变为圆锥体。对于自然腐蚀试件,频率峰值对应的VB均小于0.3,表明圆锥体锈坑比重最高。
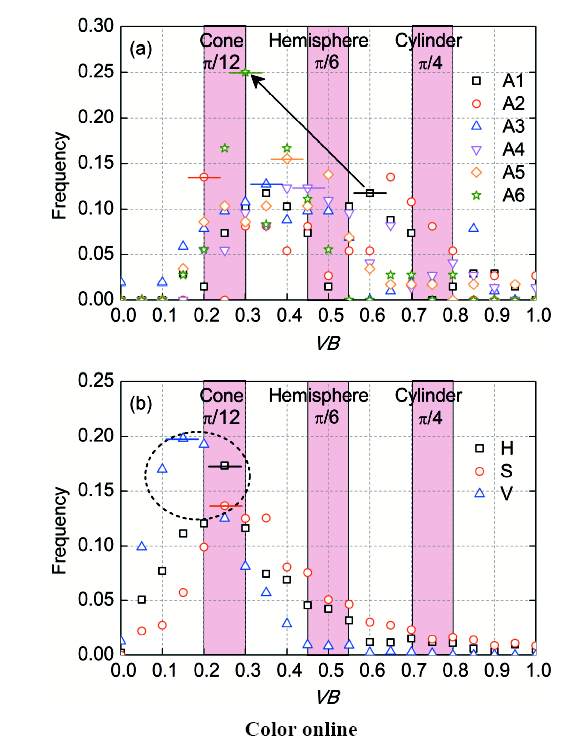
图11 锈坑形状参数(VB)统计结果
h和VB随锈蚀龄期的演变行为表明锈坑形状和深度可能存在相关关系。图12对锈坑相对深度(h'=h/hmax,hmax为锈坑深度最大值)和VB进行了汇总。为便于分析,将VB分为3个区间:I区为锥形锈坑(0~0.4),II区为半球形锈坑(0.4~0.7),III区为圆柱形锈坑(0.7~1.0)。锈坑相对深度(h'a~h'c)则被3区分为2段:h'a~h'b段包含①、②、③三部分,h'b~h'c段包含④、⑤两部分。假定散点均匀分布,则可通过特定锈坑深度区间落在I、II、III三区内面积的占比来确定锈坑形状的概率。由图12可知,锈坑不同深度对应不同形状的概率分别为:PI(0.2~0.7)=48%,PII(0.2~0.7)=40%,PIII(0.2~0.7)=12%;PI(0.7~1.0)=67%,PII(0.7~1.0)=33%。
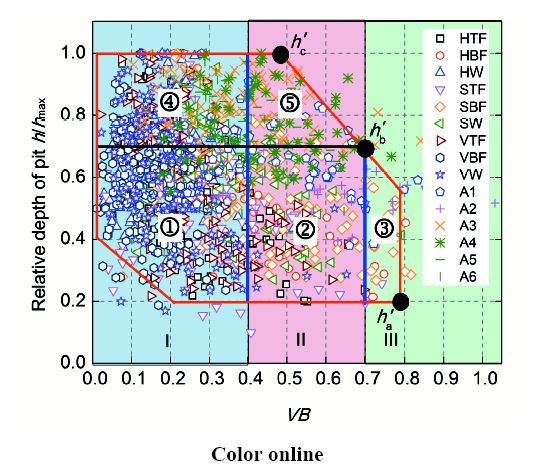
图12 锈坑深度与锈坑形状的关系
腐蚀过程中,锈坑数目是随时间变化的。根据表3中锈坑密度(Pd)统计结果可知,随着腐蚀时间的延长,相邻锈坑逐渐融合导致锈坑密度逐渐降低,这与Aziz[42]的研究结论一致;截取位置对Pd存在一定影响,竖杆(V)表面锈坑较为密集,水平杆(H)和斜杆(S)的锈坑密度则小得多,Pd随Δtave的变化规律见图13。
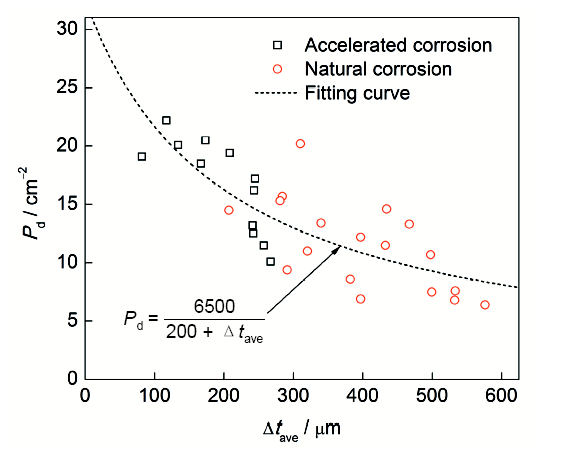
图13 锈坑密度(Pd)变化规律
3 模型建立
3.1 锈蚀深度随机场模型(SFCD)
在获取锈蚀深度随机分布特征及二维功率谱密度函数方程后,采用二维随机谐和函数写出锈蚀深度随机场函数(ζ(x, y)):
ζ(x, y)=ζ(mΔx, nΔy)=2–√∑p=0Mc-1∑q=0Nc-1[A(1)pqcos(ω1px+ω2qy+θ1pq)+A(2)pqcos(ω1px-ω2qy+θ2pq)]
(9)
A(1)pq=2S(ω1p, ω2q)Δω1Δω2−−−−−−−−−−−−−−−−−√
(10)
A(2)pq=2S(ω1p,-ω2q)Δω1Δω2−−−−−−−−−−−−−−−−−√
(11)
ω1p=pΔω1, Δω1=ω1u/Mc
(12)
ω2q=qΔω2, Δω2=ω2u/Nc
(13)
式中,m=0, 1, …, Mt-1;n=0, 1, …, Nt-1;Mt、Nt为x、y方向上生成点的数量;Δx、Δy为x、y方向上生成点的间距,单位为mm;Mc、Nc为x、y方向上的谐和分量个数;ω1u、ω2u为随机场在x、y方向上的上限截止波数;θ1pq、θ2pq为均匀分布在[0, 2π]之间的随机相位角;ω1u、ω2u由以下准则进行确定[43]:
∫ω1u0∫ω2u-ω2uS(ω1, ω2)dω1dω2=(1-∈)∫∞0∫∞-∞S(ω1, ω2)dω1dω2
(14)
其中,∈≪1,例如0.001。已知上限截止波数ω1u、ω2u及生成表面的尺寸(Lx, Ly),谐和分量个数Mc、Nc由下式确定:
⎧⎩⎨Δω1=2πLxΔω2=2πLy
(15)
{Mc=ω1uΔω1Nc=ω2uΔω2
(16)
为避免频谱混叠现象,生成点的间距和数量做如下规定[43]:
{Δx≤2π2ω1uΔy≤2π2ω2u
(17)
{Mt≥2McNt≥2Nc
(18)
由式(15)~(18)可知,ω1u、ω2u的取值决定了生成网格的间距、表面起伏的波长及周期特征,其反映了腐蚀表面的相关长度,对腐蚀表面具有重要影响。
根据式(5)和(9),腐蚀表面进一步表示为:
z(x, y)=ζ(x, y)-Δtave
(19)
3.2 锈坑随机分布模型(RDCP)
在Cartesian空间(x, y, z)中,单锈坑表面可由以下方程描述:
Ssp(x, y)={Θ (x, y)∈Ω0 (x, y)∉Ω
(20)
Θ(x, y, x0, y0, h, r)=⎧⎩⎨⎪⎪⎪⎪⎪⎪⎪⎪hr(x-x0)2+(y-y0)2−−−−−−−−−−−−−√-h (Corn)-hrr2-(x-x0)2-(y-y0)2−−−−−−−−−−−−−−√ (Hemisphere)-h (Cylinder)
(21)
式中,Ω为单个锈坑坐标范围;Θ为锈坑形状方程;r为锈坑半径,r=0.5hAr;(x0, y0)为z=0平面的圆心坐标,用于确定锈坑位置;h、r、x0、y0均为随机变量。
根据锈坑参数统计结果,h、Ar及数量(Np)由下式生成:
⎧⎩⎨⎪⎪⎪⎪h=lognrnd(μh, σh, Np)Ar=lognrnd(μAr, σAr, Np)Np=PdA
(22)
式中,lognrnd为对数正态分布随机函数;A为板材表面面积(LxLy)。将随机生成的锈坑深度进行升序排列,根据图12可确定不同形状锈坑的数量。
锈坑位置坐标(x0, y0)在板材表面区间(Lx, Ly)上随机生成:
{x0=random(0, Lx)y0=random(0, Ly)
(23)
同一个表面上可能存在多个锈坑,将第i个锈坑Θ(i)对应的表面记作S(i)sp,则多锈坑表面可表示为多个单锈坑表面的交集,从而建立锈坑随机分布模型(RDCP):
S(x, y)=S(1)sp⋂S(2)sp⋂⋅⋅⋅⋂S(Np)sp=⋂1NpS(Np)sp
(24)
腐蚀表面则进一步表示为:
z(x, y)=S(x, y)+∣∣∣∣S̅(x, y)∣∣∣∣-Δtave
(25)
式中,S̅(x, y)为生成表面S(x, y)锈蚀深度的平均值。
3.3 腐蚀表面映射重建
基于上述腐蚀表面统计特征与随机模型可实现腐蚀表面模拟与大规模映射重建。以SFCD模型为例,说明腐蚀表面重建过程:(1) 利用平均锈蚀深度(Δtave)由图6和8确定锈蚀深度标准差(tsd)和功率谱密度参数(κ1, κ2);(2) 将tsd、κ1、κ2代入式(8)和(14),确定上限截止波数(ω1u, ω2u);(3) 将表面尺寸(Lx, Ly)和ω1u、ω2u代入式(15)~(18),确定谐和分量个数(Mc, Nc)、点间距(Δx, Δy)和点数量(Mt, Nt);(4) 将以上信息代入SFCD模型,即式(8)~(13),生成对应Δtave的腐蚀表面。
类似地,将Pd、h、Ar、形状等锈坑参数统计结果代入式(20)~(25),可实现基于RDCP模型的腐蚀表面模拟与重建。
为验证模型的有效性,图14给出了基于SFCD和RDCP模型重建的试件HTF的表面形貌,并与Silva等[27]的模型进行了对比。由图可知,Silva模型模拟结果并不理想,其主要原因为:(1) 模型基于海洋环境提出,腐蚀变量均假定为正态分布,对一般大气环境不具有普适性;(2) 腐蚀深度采用random函数随机生成,忽略了腐蚀深度相关长度,无法准确表征腐蚀表面起伏特征;(3) 将锈坑简化为理想半椭球体,无法反映锈坑形状的变异性与锈坑参数的内在相关性。而本模型充分考虑了一般大气环境结构钢腐蚀表面特征参数的变化规律与内在联系,克服了既有模型中存在的上述缺陷,因而重建表面在形貌特征上表现出更高的还原度。
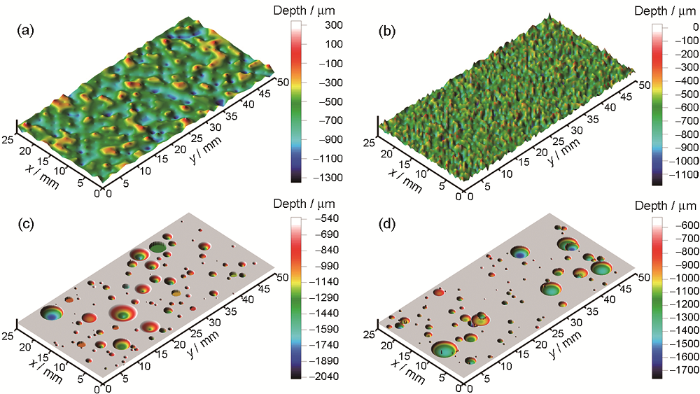
图14 HTF试件(Side B)映射重建形貌
4 结论
(1) 提出了用于锈蚀钢材表面表征的基本参数及提取方法,通过对锈蚀深度和锈坑特征参数提取结果进行统计分析发现:锈蚀深度服从正态分布,锈坑深度(h)与径深比(Ar)服从对数正态分布;随着腐蚀程度的增大,锈蚀深度均值(Δtave)、锈蚀深度标准差(tsd)、锈蚀深度功率谱密度峰值、锈坑深度对数均值(μh)逐渐增大,锈坑径深比对数均值(μAr)逐渐减小;锈坑形状与锈坑深度存在相关关系,并由圆柱体和半球体逐渐向圆锥体转变。
(2) 基于统计分析结果,建立了锈蚀深度随机场模型与锈坑随机分布模型,实现了一般大气环境锈蚀钢材表面特征的准确表征和模拟。与既有模型相比,本模型充分考虑一般大气环境结构钢腐蚀表面特征参数的变化规律与内在联系,克服了既有模型内在缺陷,重建形貌还原度更高。
免责声明:本网站所转载的文字、图片与视频资料版权归原创作者所有,如果涉及侵权,请第一时间联系本网删除。

官方微信
《中国腐蚀与防护网电子期刊》征订启事
- 投稿联系:编辑部
- 电话:010-62316606-806
- 邮箱:fsfhzy666@163.com
- 中国腐蚀与防护网官方QQ群:140808414





